二叉树理论知识
定义
二叉树是一种树形数据结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。
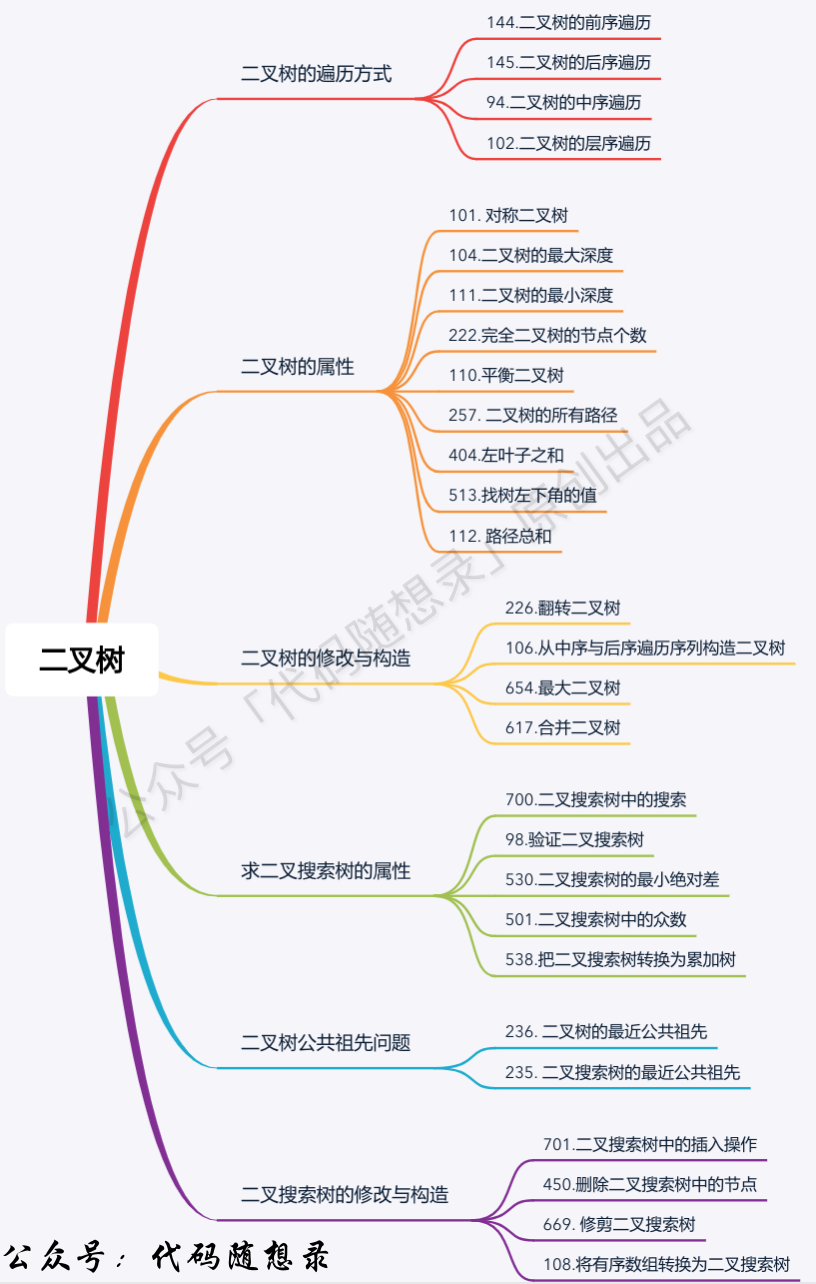
基本定义:
二叉树是一个递归定义的数据结构,它要么是一棵空树,要么是一棵由一个根节点和两棵互不相交的二叉树(左子树和右子树)组成的非空树
结构特点:
有序性: 二叉树的左子树和右子树是有序的,左子树在前面,右子树在后面
子树互斥: 左子树和右子树也是二叉树,并且互不重叠
节点数量限制: 每个节点最多有两个子节点,不存在度大于2的节点
特殊类型:
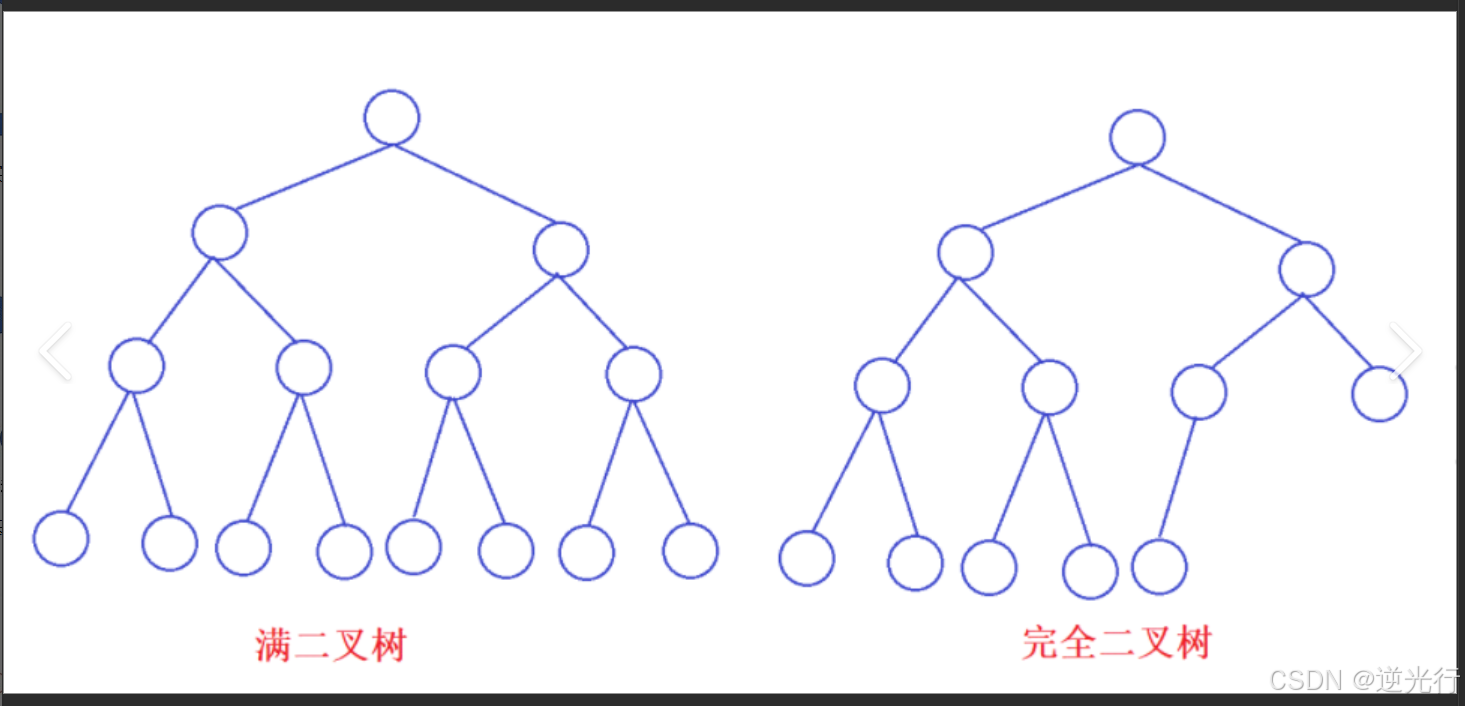
满二叉树: 所有分支节点都存在左子树和右子树,并且所有叶子节点都在同一层上
完全二叉树: 按层序编号,如果编号为i的节点与深度相同的满二叉树中编号为i的节点位置完全相同,则称为完全二叉树
斜树: 所有节点都只有左子树的称为左斜树,所有节点都只有右子树的称为右斜树
存储结构:
顺序存储: 使用数组存储,适合表示完全二叉树,但不适用于非完全二叉树,因为非完全二叉树会有空间浪费
链式存储: 使用链表表示,每个节点包含数据域和两个指针域,分别指向左孩子和右孩子